Line Intersecting A Polygon

Being able to detect when a line is intersecting a plane will be useful, but I thought next I would have a go at detecting a more specific case: whether or not a line is intersecting a polygon.

For this, I used the same set-up as before: a simple 2D triangle and a line that changes colour based on whether it is intersecting the triangle. Because a line can only be intersecting a polygon if it intersects the plane that the triangle lies on, the code from the program before was reused. First the plane intersection is performed. If the test fails, the line cannot be intersecting the polygon so we are done. If the line is intersecting the plane, we need to perform more analysis to determine if it intersects the polygon.

In order to do this, we first need to determine the point on the plane that the line is intersecting. For this, we need to utilise a vector operation known as the dot product. For arbitrary vectors a and b, the dot product is defined as the following:

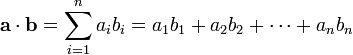
That is, each component of a vector is multiplied together and summed, returning a single value. Given two vectors A and B that represent points in 3D space, the dot product is found by performing the following calculation.

Geometrically speaking, the dot product represents an operation on the length of the vectors and the angle between them. A geometric interpretation of the dot product is as follows:

That is, performing the dot product gives us the lengths of the two vectors multiplied and then multiplied again by the angle between the two vectors. This proves to be a very useful equation for probing the geometric relationship between two vectors. For now, observe that if both vectors a and b are unit vectors, their product will simply be one, meaning that the dot product of two unit vectors will actually give you the cosine of the angle between them.

So how can we use this information to find the point that the line intersects the plane at? Firstly we need a representation of the line to work with so we obtain the line's vector by subtracting one endpoint of the line from the other endpoint. Now that we have the line's vector, we need to find the point at which the vector intersects the plane that the polygon lies on. The first step is to choose one of the line's endpoints and find the   closest distance that it lies from the plane. This is achieved by substituting the endpoint's coordinates into the equation for the plane. We negate the distance value as we want to move back along the vector. This distance is also the magnitude of a vector that shoots perpendicular from the plane to the line's endpoint. Since the normal of the plane is also perpendicular to the plane, the vector from the plane to the endpoint and the plane normal share an orientation. Because of this, we can perform a dot product operation between the normal of the plane and the line's vector to find the angle between the line and the vector from the plane to the line endpoint. After performing these two operations, we now have the angle and the length of one side of the triangle formed between the plane and the line. This is demonstrated below.

Here, we can see that the Line vector L and the Plane Normal N (in the reverse direction because we negated the distance) form a triangle. The use of the plane equation and the dot product have given us the length of one side (-d) and the angle between two of its sides (θ). What we want to find is the magnitude of the side of the triangle from the line endpoint L1 to the intersection point i. This just comes down to basic trigonometry. Since we want to find the length of the hypotenuse and we know the length of the side adjacent to the angle, the length of the hypotenuse can be found by:

This distance tells us how far along the line vector we need to move until we reach the point that intersects with the plane. Geometrically, multiplying a vector by a scalar means moving along the vector. Because of this, in order to obtain the intersection point, we take our endpoint, L1 and add on the line vector multiplied by the magnitude of the distance from L1 to i. This effectively means we start at L1 and move along the vector until we get i.

Now that we have the coordinates of the point where the line intersects with the plane, we have one final step: to determine if that point lies inside of the polygon. To determine the "insidedness" of the point, a simple trick can be performed. Firstly, we visualise drawing lines from each pair of the polygon's vertices to the intersection point. Each pair of lines forms a triangle. This is illustrated in the figure below.

The key to this solution is realising that the angles around the intersection point formed by each of the triangles should all add up to 360 degrees. If the angles do not add up to 360 degrees, the point is not inside the polygon and we can return false otherwise the point is inside the polygon and we can return true. How to construct the triangles within the polygon and find the sum of their angles? The first step is to take two of the vertices and create two vectors originating from the intersection point. This can be done by taking the vertex coordinates and subtracting the coordinates of the intersection point. After normalising, our trusty dot product operation can then be used to find the angle between the two vectors and thus one of the interior angles around the intersection point. Repeating this for each of the polygon vertex pairs and totalling the angles found mean we will be able to determine if the intersection lies inside the polygon or not.

Images: Wikipedia
Images and 3D "insidedness" algorithm: http://paulbourke.net/geometry/insidepoly/